![\[ \begin{array}{c} p=at^3 + bt^2 + ct + d \\ p' (0)=g (p_1-p_0) \\ p' (1)=g (p_3-p_2) \end{array} \]](form_0.png)
This page is a result of me finding hardly any very useful documentation about cubic tensor product patches
and how to subdivide them easily. It is also a convenient place for me to go to in order to re-learn what I keep forgetting.
It is a part of the Laxkit documentation.
By Tom Lechner. This page is released under the
Creative Commons Attribution Non-Commercial Share-Alike license.
![\[ \begin{array}{c} p=at^3 + bt^2 + ct + d \\ p' (0)=g (p_1-p_0) \\ p' (1)=g (p_3-p_2) \end{array} \]](form_0.png)
If we take g=3, then we have the most common type of this sort of cubic curve. So from the above we find:
![\[ p=(-p_0+3p_1-3p_2+p_3)t^3 + (3p_0-6p_1+3p_2)t^2 + (-3p_0+3p_1)t + p_0 \]](form_1.png)
or
![\[ \begin{array}{c} \left[\begin{array}{c} p_x \\ p_y \end{array}\right] = \left[\begin{array}{cccc} p_{0x} & p_{1x} & p_{2x} & p_{3x} \\ p_{0y} & p_{1y} & p_{2y} & p_{3y} \end{array}\right] \: \left[\begin{array}{cccc} -1 & 3 & -3 & 1 \\ 3 & -6 & 3 & 0 \\ -3 & 3 & 0 & 0 \\ 1 & 0 & 0 & 0 \end{array}\right] \: \left[\begin{array}{c} t^3 \\ t^2 \\ t \\ 1 \end{array}\right] \\ \\ P=G\; B\; T \end{array} \]](form_2.png)
Note that  .
.
This curve has the convenient subdividable property that with points p0 to p3, we can subdivide this so that we have 2 new segments whose points are [p0 q1 q2 q6] and [q6 q4 q5 p3]. Note also that a bezier segment will always be contained within the bouning box of the vertex and control points. More specifically, the curve will always be contained within the convex hull of those points.
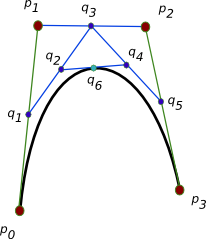
 , it follows that the length of the vector connecting a vertex point and its control point is v:
, it follows that the length of the vector connecting a vertex point and its control point is v:
![\[ v=\frac{4\:r}{3}\:\frac{2\;sin(\theta/2)-sin(\theta)}{1-cos(\theta)} \]](form_5.png)
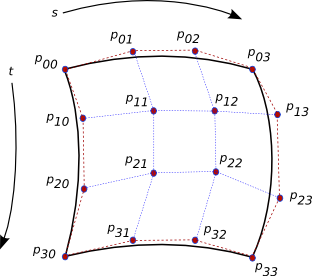
![\[ P\:=\:S^T\:B\:G^T\:\:B\:T \]](form_6.png)
![\[ S=\left[\begin{array}{c} s^3 \\ s^2 \\ s \\ 1 \end{array}\right],\: G= \left[\begin{array}{cccc} p_{00} & p_{01} & p_{02} & p_{03} \\ p_{10} & p_{11} & p_{12} & p_{13} \\ p_{20} & p_{21} & p_{22} & p_{23} \\ p_{30} & p_{31} & p_{32} & p_{33} \end{array}\right],\: T=\left[\begin{array}{c} t^3 \\ t^2 \\ t \\ 1 \end{array}\right] \]](form_7.png)
where p are either the x or y coordinates of the points, depending on whether you want the x or y coordinate of P.
(*** TODO: explain where the hell that patch equation came from)
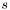 and
and 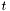 that each run from 0 to 1. You want a section of the patch as a function of
that each run from 0 to 1. You want a section of the patch as a function of 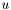 and
and 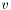 which also run from 0 to 1.
which also run from 0 to 1.
For 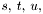 and
and 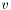 , make corresponding matrices:
, make corresponding matrices:
![\[ S=\left[\begin{array}{c} s^3 \\ s^2 \\ s \\ 1 \end{array}\right],\: T=\left[\begin{array}{c} t^3 \\ t^2 \\ t \\ 1 \end{array}\right],\: U=\left[\begin{array}{c} u^3 \\ u^2 \\ u \\ 1 \end{array}\right],\: V=\left[\begin{array}{c} v^3 \\ v^2 \\ v \\ 1 \end{array}\right] \]](form_13.png)
These will be linearly related to 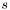 and
and 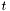 like this:
like this:
![\[ v=n (t-t_0),\;t=v/n + t_0, \:\:\:\:\:\: u=n (s-s_0),\;s=u/m + s_0 \]](form_14.png)
So 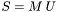 , and
, and 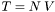 where:
where:
![\[ M= \left[\begin{array}{cccc} 1/m^3 & 3 s_0/m^2 & 3 s_0^2/m & s_0^3 \\ 0 & 1/m^2 & 2 s_0/m & s_0^2 \\ 0 & 0 & 1/m & s_0 \\ 0 & 0 & 0 & 1 \end{array}\right], \:\: N= \left[\begin{array}{cccc} 1/n^3 & 3 t_0/n^2 & 3 t_0^2/n & t_0^3 \\ 0 & 1/n^2 & 2 t_0/n & t_0^2 \\ 0 & 0 & 1/n & t_0 \\ 0 & 0 & 0 & 1 \end{array}\right] \]](form_17.png)
Use those plus the above equation for a patch and get points Q:
![\[ Q\:=\:U^T\:B\:G_q^T\:\:B\:V \]](form_18.png)
![\[ Q\:=\:U^T\:B^T\:(((B^{-1})^T\:M^T\:B)\:G^T\:(B\:N\:B^{-1}))\:B\:V \]](form_19.png)
![\[ G_q^T\:=(((B^{-1})^T\:M^T\:B)\:G^T\:(B\:N\:B^{-1})) \]](form_20.png)
where 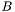 is the plain bezier curve matrix,
is the plain bezier curve matrix, 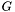 is the coordinate matrix of the original patch as above, and
is the coordinate matrix of the original patch as above, and 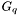 magically contains the coordinate matrix of the new patch for u and v.
magically contains the coordinate matrix of the new patch for u and v.
 1.4.6
1.4.6